外角の求め方 外角の求め方を下記に示します。 外角=外角と隣り合わない内角の和 例えば下図の三角形の外角=3050=80度です。上式を覚えておけば簡単に外角が算定できます。 なぜ外角=外角と隣り合わない内角の和となるか解説します。式area = 1/2 * base * heightを使用して各三角形の面積を計算します。不規則な五角形の総面積を調べるためにすべての面積を加えます。 図の一部ではない部分がある場合は、正五角形の面積を求めます。総面積の欠けている部分の面積を引きます。今回から練習を始めた『 面積測定の使い方 』のポイントは、その計算方法を理解することが大切です。 通常の計算では、縦×横=で面積は計算しますが、ここで紹介している面積の計算方法は俗に言う『 三斜法 』で計算されます。
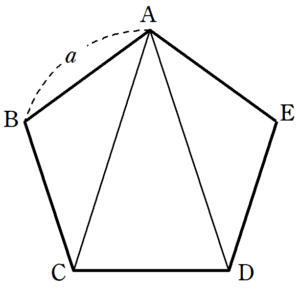
正多角形の面積の公式 Fukusukeの数学めも
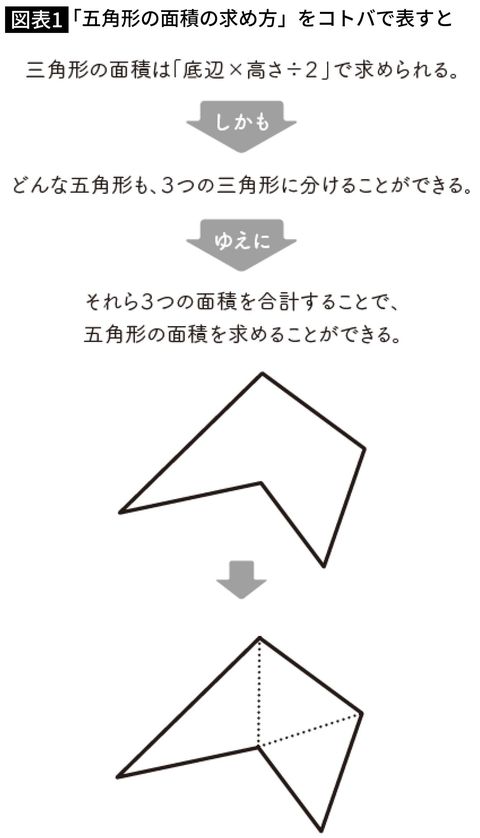
五角形の面積の求め方
五角形の面積の求め方-5年 学研教育情報資料センター 算数 学習相談 小/算数/5年/量と測定/ 四角形・三角形の面積/理解シート等積変形の基本性質 平行な線に挟まれている三角形は、底辺の大きさが等しければ面積が等しくなる。 これが、平行線と面積に関する基本性質です。 でも、なんで面積が等しくなるの? ? それはね! 平行線は、どこを取っても距離が等しくなるよね。 だから、平行線に挟まれている三角形は どれも高さが等しいということになるんだ。



正五角形の面積
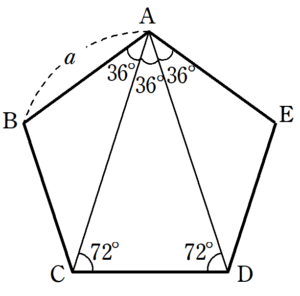
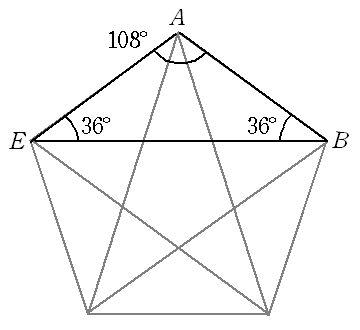
正多角形の内角の求め方 を解説していくよ。 よかったら参考にしてみてね^^ 4秒で計算できる! 正多角形の内角の公式 正多角形の1つの内角の大きさを求めたいときは、 つぎの公式をつかってみて。 正n角形の1つの内角は、 ちゃんと求めるには、無理数になってしまいますけど、面積の求め方という点で言えば、次のように言えばいいと思います。 三角形の面積が 底辺×高さ÷2であることが理解できていると仮定します。 式から 正五角形の場合だけ 「1辺の長さ」と「対角線の長さ」の比を求めてください その絵のちょうどど真ん中にある「頂角 36度」の大きな二等辺三角形 (とその中にある対角線) を使うのがお
正五角形の面積 中三程度で理解できるように、根号と三平方の定理までを使用し、三角関数は使用していません。 三角関数で解く場合はこちらを参照してください。 1)外接円の半径がわかっているとき次図のような三角形の面積を座標法によって求める場合を考えると次のようになる。 前図の三角形の面積を求める場合、次図のように「赤い四角形」から「青い四角形」を引けばよ いことが解る。 まず、赤い四角形の面積を考える。 平行四辺形の面積は「底辺×高さ」で求められたよね?? 菱形は平行四辺形ともいえるから、 この面積の公式も使えちゃうってわけさ。 じゃんじゃん計算していこう!! まとめ:ひし形の面積の求め方は2通りおさえよう! ひし形の面積の求め方は、 対角
約5年前 多角形の面積は、 ①直線を引いて三角形や四角形に分ける ②周りを線で囲んで、要らない部分の面積を引く この2種類の方法があります! ②の方法は六角形くらいが限度と思います。 ①の方法で直角を作るのが難しい時に使うのがオススメです。 最終手段として考えておくのが妥当ですが。 雪音鈴**study 約5年前 正方形や長方形の面積は、\(「面積=たての長さ×横の長さ」\) で求められます。 例題「1辺の長さ \(4cm\) の正方形」の面積と「たての長さ \(3cm\),横の長さ \(5cm\) の長方形」の面積を求めてください。面の形は正三角形なので「面の辺の数は3」、正二十面体なので「面の数は」、1点に集まる面の数「5」。 ⇒(辺の数)= 3 × ÷ 5 =12 1点に集まる面の数は少しややこしいですが、これさえ分かれば簡単に正多面体の頂点の数を求められるのです。



正五角形の面積 東海 2004 どう解く 中学受験算数




最も好ましい 五角形 の 面積 の 求め 方 シモネタ
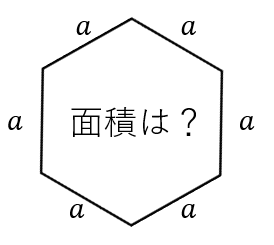
正多角形の面積の公式 1辺の長さを a ~a~ a とした、正三角形から正六角形までの面積を求めます。 Ⅰ 面積の公式 Ⅱ 面積の公式の証明 Ⅰ 面積の公式 1辺 a ~a~ a の正四角形(正方形) と求まる。 三角比の値が、手計算でわかる n ~n~ n の値は、 n = 3, 4次の立体の体積を求めましょう 問題① 底面の形は五角形です 底面を上から見ると 3つの三角形を切り離して、わかりやすく方向を回転させると 3つの三角形の面積を求めます 黄色の面積 10×3÷2=15 きみどりの面積 10×5÷2=25 オレンジの面積 8×3÷2=12 合計すると 15+25+12=52 (底面積) 一般の五角形の面積は三角形3個に分けて求めます。 正5角形の面積は、1辺の長さが a の場合に 5×(aの2乗)÷(4×tan(π/5)) です。 πは円周率、tanはタンジェントです。



1
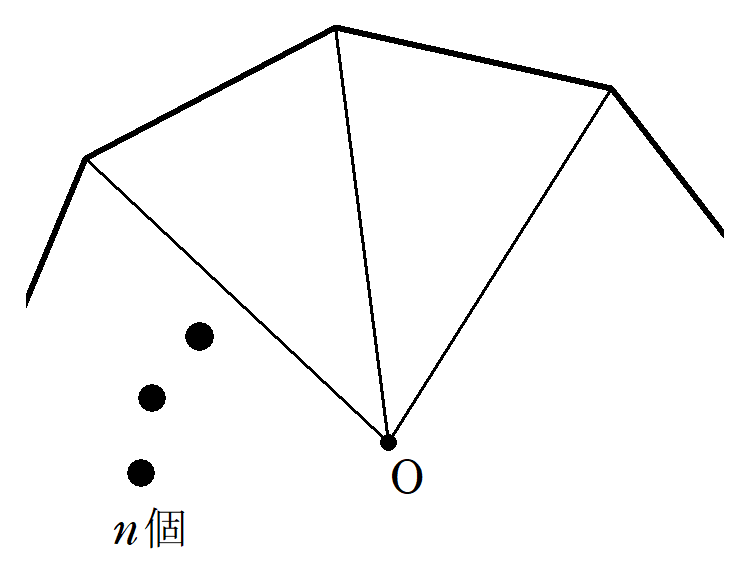



正多角形の面積の公式 一般化 Fukusukeの数学めも
五角形の面積を等積変形で求めるMaster plan €定 ab . € a € b Designed by Y uchi & S Yamamoto, 1.学習の題材 授業コンセプト 対象学年:中学校2年生~ 三角比を使わないのなら、正五角形の1辺と対角線の比が1: (1+√5)/2 になることから、等しい辺がaで底辺が (1+√5)a/2の二等辺三角形2つ と、等しい辺が (1+√5)a/2で、底辺がaの二等辺三角形1つを合わせて (高さは三平方の定理から求め) 面積= (a^2/4) {√ (10+2√5)+√ (5+2√5)} です。 1人 がナイス! しています ナイス! https//detailchiebukuroyahoocojp/qa点cを中心に直線chの長さを半径とする弧を描き、円との交点iを求める。 (5) コンパスで直線chの長さで円に交点を求め直線で結ぶと、正五角形の完成。 多角形52/分度器と直線定規を使った正五角形の描き方 分度器や直線定規を使った、円に内接する「正




正多角形の面積の公式 Fukusukeの数学めも




多角形の内角の和 は何度なのか を説明します おかわりドリル
定義や公式(面積の求め方)、面積比の計算問題 五角形以上の面積 そして、五角形以上の多角形の面積を求める場合には、 問題に合わせて対処 するようにしましょう。正五角形の面積を求める2つの公式 具体例で学ぶ数学 > 図形 > 正五角形の面積を求める2つの公式 最終更新日 中心から頂点までの距離が R である正五角形の面積は、 5 R 2 8 10 2 5 ≃ 238 R 2 一辺の長さが a である正五角形の面積は、 a 2 4 25 10 5 ≃ 2本の対角線の長さ a, b と対角線の交わる角度 θ が分かっている場合、その四角形の面積 S は S = 1 2 a b sin θ で求められます。 関連記事 三角関数の基礎知識。 sinθ cosθ tanθ の覚え方・弧度法・三角比の表まとめ たとえば、「2本の対角線の長さが 8




小5 算数 小5 33 五角形 六角形 多角形 Youtube




通常の五角形の面積を求める 3つの方法 Wikihow
ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と 五角形の内角の和: 540° 540 ° 六角形の内角の和: 7° 7 ° ・・・ n角形の内角の和: 180°× (n−2) 180 ° × ( n − 2 ) この公式は覚えやすいので暗記してもいいのですが、簡単に導出できるため、わざわざ覚える必要もありません。 ではどのようにこの公式を導出するのか、なぜ内角の和が「 180°× (n −2) 180 ° × ( n − 2 ) 」になるのか、 (n−2 赤+黄色の部分 と ABCDE内の白い部分 の対決 です。 正五角形の面積をSとします。 赤い部分の面積 五角形ABCDEとFGHIJは相似なので相似比ABGH=1\( \frac{3\sqrt5}{2}\)より 面積比は1\(\frac{146\sqrt5}{4}\) よって赤い部分の面積は\( \frac{73\sqrt5}{2}S \)




簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく



1
既習事項の確認をする。 「星形五角形の角の和」 している。(関心・意欲・態 星形六角形や七角形をノートに 書かせる。 課題を提示する。 ①n=6のとき、星形六角形の角を求 めよう。 ②n=7のとき、星形七角形の角を求 めよう。三角柱や四角柱などの体積は、底面積 $S$、高さ $h$ として、次の式で求められます。 角柱 (かくちゅう) の体積 \begin{align*} V = Sh \end{align*} 体積 = 底面積 × 高さ1 辺の長さが分かっている時は公式を用いる 基本の六角形は6つの二等辺三角形で構成されているので、その公式もまた二等辺三角形の面積を求める公式が元になっています。 六角形の面積(A)を求める公式は A = (3√3 s2)/ 2 となり、 s が辺の長さを指しています。 {"smallUrl""https\/\/wwwwikihowcom\/images_en\/thumb\/e\/eb\/CalculatetheAreaofa



正五角形の面積について1辺の長さが1である正五角形の面積を求めた Yahoo 知恵袋




最も好ましい 五角形 の 面積 の 求め 方 シモネタ
面積を求める手順 各頂点の座標を求める ①で求めた座標から長さを求める ②で求めた長さを使って面積を求める 多くの人が座標を求めるという1ステップ目でつまづいてしまいます。 ですが、座標を乗り切ったらもうゴールは目の前です。 面積を求めるのが苦手だという方は、まずは座標を求める練習に力を入れてみてはいかがでしょうか。 > 一次関数 例えば、1つ目の辺が5センチ、次が4センチ、次が7センチ、次が3センチ、あと残りは10センチの場合、以下の計算で周囲は 60センチとなります。 周囲= 5 4 7 3 10 10 10 10 = 60 cm 4 次は面積の出し方です。 この写真をみてください。 緑の線は中心から八角形の線に向かって垂直に引かれています。 この線の長さを測ると10センチでした。 この場合相似な図形の面積の比は「相似比の \(2\) 乗の比」になります。 つまり、 相似比 \(ab\) の図形の面積の比は \(a^2b^2\) です。 なので 面積の比は \(a×ab×b\) となるわけです。 もちろん、三角形だけでなく、円や四角形や五角形やその他なんでも



五芒星の面積の考え方 希望的観測日記 ブログ枝部



不規則な五角形の面積の求め方を教えて下さい 不規則な五角形 平 Yahoo 知恵袋
・四角形の面積を三角形分 割の考えで求めること ができる。(考) <数と計算> 6年 円の面積 ・円の面積の求め方を 考えることができ る。(考) 第6学年 単元名「立体の体積」 ~直方体の体積やいろいろな図形の面積を求める考え方とつないで~三角形 (さんかくけい) の 面積 (めんせき) の求め方の 基本 (きほん) は「 底辺 (ていへん) × 高 (たか) さ ÷ 2」ですが、高さが分からないときに 他 (た) の 情報 (じょうほう) から面積を求める 公式 (こうしき) がいくつもあります。



正五角形の面積



面積の公式をつくろう



不規則な五角形の面積の求め方を教えて下さい 不規則な五角形 平 Yahoo 知恵袋



図形 正五角形の分解 父ちゃんが教えたるっ




正多角形の面積から円の面積の公式へ 算数を究める



多角形の面積の公式を教えてください 中学生なんでよければわか Yahoo 知恵袋




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく



不規則な五角形の面積の求め方を教えて下さい 不規則な五角形 平 Yahoo 知恵袋
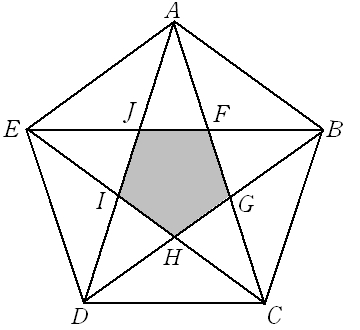



茗渓予備校 科目情報



正五角形の面積



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典



五芒星の面積の考え方 希望的観測日記 ブログ枝部



正多角形の面積の公式 Fukusukeの数学めも




図の斜線部の面積の求め方をおしえてください 正五角形で一辺の長さをaとする Clearnote




つくばサイエンスエッジ18 文京学院大学女子高校 みらいぶ 高校生サイト




多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト



2




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun



面積比の問題です 教えてくださいm M 問題 図 Yahoo 知恵袋




多角形の内角の和 は何度なのか を説明します おかわりドリル




高校数学b ベクトルと正五角形 Cos108 の値 受験の月



不規則な五角形の面積の求め方を教えて下さい 不規則な五角形 平 Yahoo 知恵袋




五角形abcdeと面積が等しい四角形abcfをつくる問題です 分からないので Clearnote



円周率とは何か と聞かれて 3 14です は大間違いである それでは答えになっていない 2ページ目 President Online プレジデントオンライン




高校数学 正多角形の面積の求め方 練習編 映像授業のtry It トライイット



定法 正五角形の面積 雑学のソムリエ
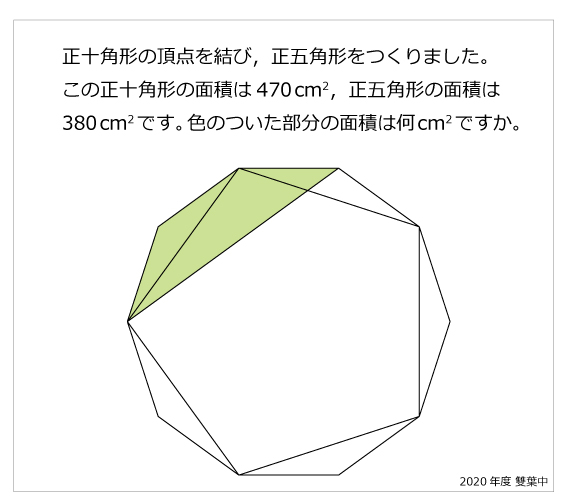



雙葉中 正五角形と正十角形年雙葉中 正五角形と正十角形 算数星人のweb問題集 中学受験算数の問題に挑戦
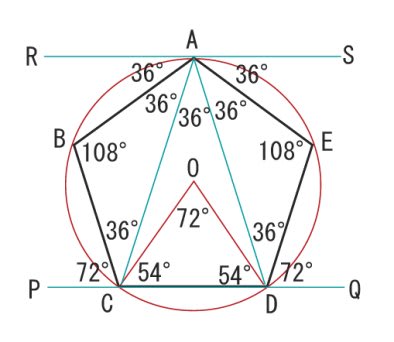



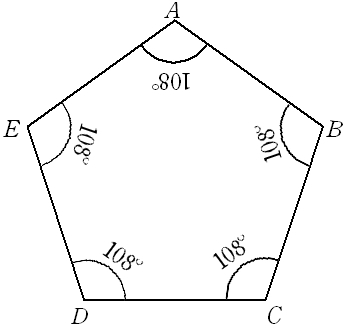
正五角形というだけで 分かる角度は 名寄 算数数学教室より
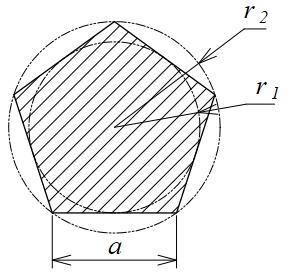



正多角形の断面積 内外接円 断面二次モーメント 断面係数の公式と計算フォーム 機械技術ノート




通常の五角形の面積を求める 3つの方法 Wikihow



正五角形と円弧 女子学院中学 受験算数問題 2000 どう解く 中学受験算数




通常の五角形の面積を求める 3つの方法 Wikihow
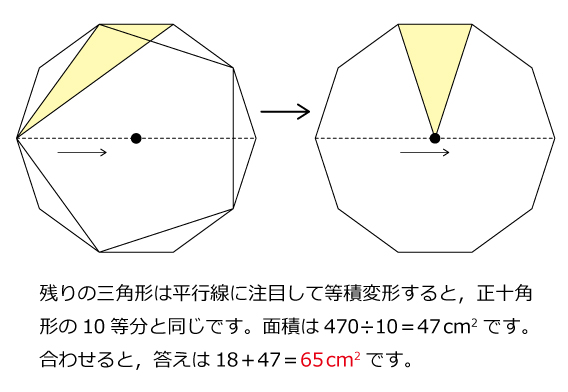



雙葉中 正五角形と正十角形年雙葉中 正五角形と正十角形 算数星人のweb問題集 中学受験算数の問題に挑戦




教えてください Clearnote




最も好ましい 五角形 の 面積 の 求め 方 シモネタ
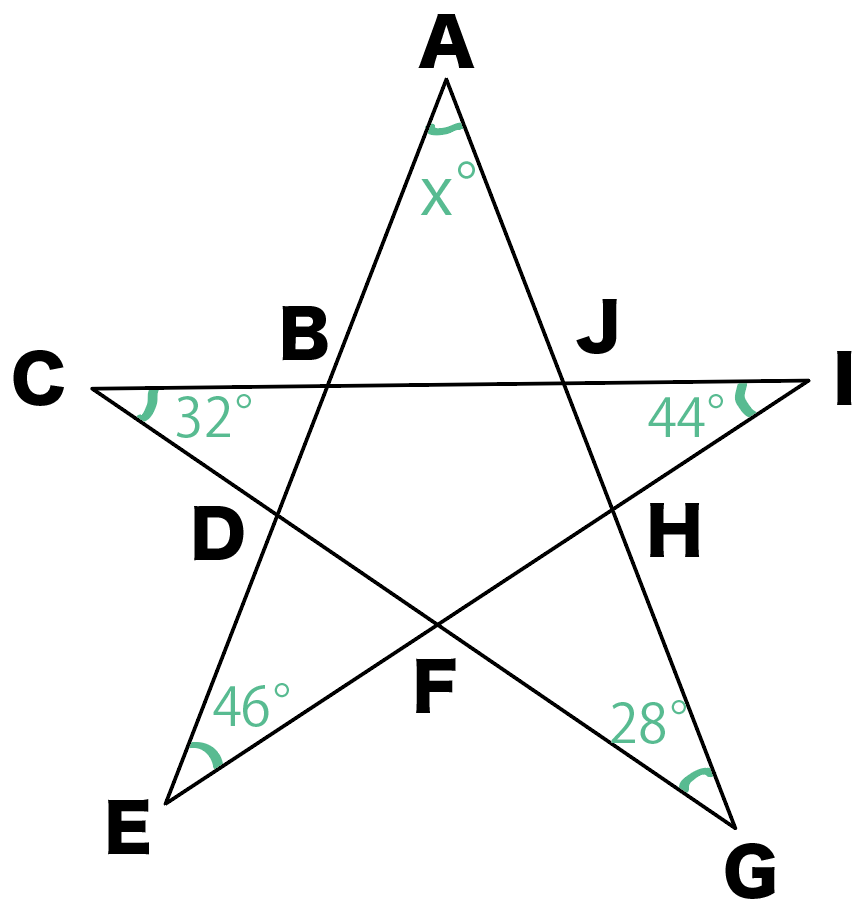



星形の角度の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




五角形の面積の求め方を教えて下さい Clearnote



最も好ましい 五角形 の 面積 の 求め 方 シモネタ




相似19 正五角形と黄金比 Youtube




相似19 正五角形と黄金比 Youtube



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典




多角形の内角の和 算数の公式覚えてますか




通常の五角形の面積を求める 3つの方法 Wikihow




多角形の内角の和の公式と外角の和を利用した角度の求め方
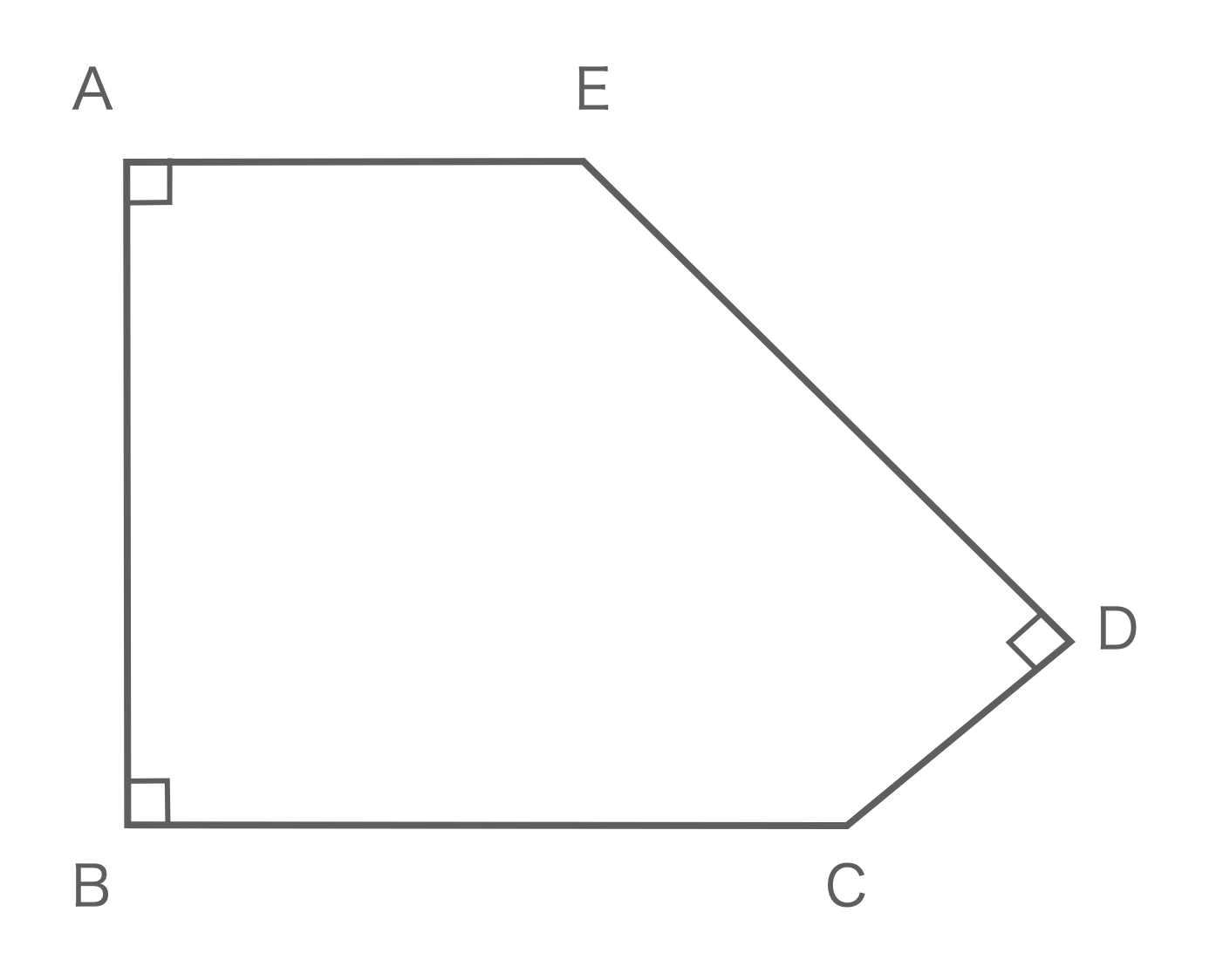



最も好ましい 五角形 の 面積 の 求め 方 シモネタ




つくばサイエンスエッジ18 文京学院大学女子高校 みらいぶ 高校生サイト



1
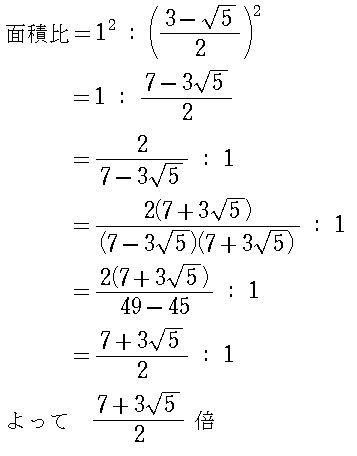



茗渓予備校 科目情報




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



定法 正五角形の面積 雑学のソムリエ
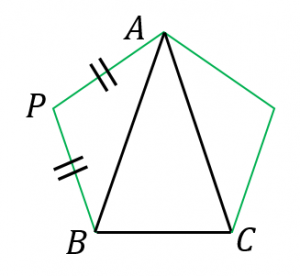



正五角形の対角線の長さと高さ 具体例で学ぶ数学



不規則な五角形の面積の求め方を教えて下さい 不規則な五角形 平 Yahoo 知恵袋




正多角形の面積の公式 Fukusukeの数学めも




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典



6年算数 円柱と角柱の体積 教え方2



1
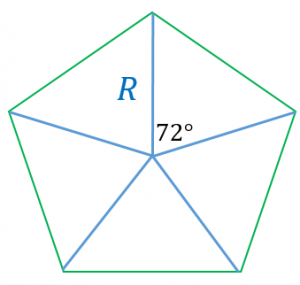



正五角形の面積を求める2つの公式 具体例で学ぶ数学



図形 正五角形の分解 父ちゃんが教えたるっ




正五角形の長さや面積の導出 数学の偏差値を上げて合格を目指す



五芒星の面積の考え方 希望的観測日記 ブログ枝部



茗渓予備校 科目情報




通常の五角形の面積を求める 3つの方法 Wikihow



正六角形の面積 計算ツール 公式の導出 具体例で学ぶ数学




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
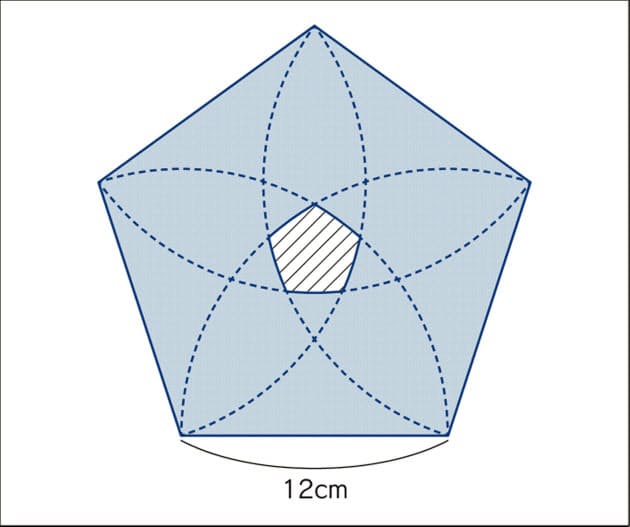



算数オリンピックに挑戦 第23回 Nikkei Style




17年6月のブログ記事一覧 4ページ目 身勝手な主張



茗渓予備校 科目情報




多角形の内角の和 算数の公式覚えてますか
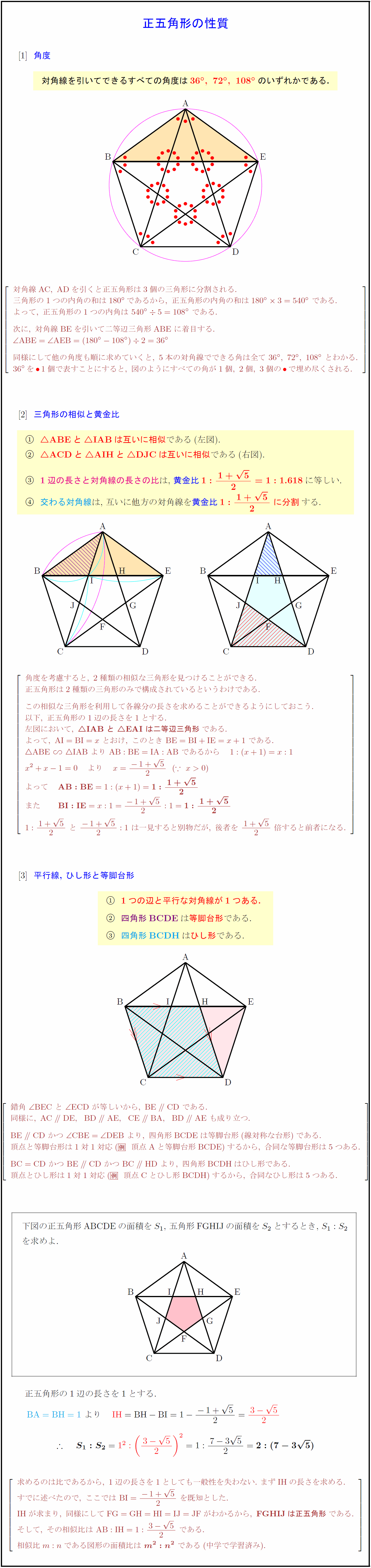



高校数学a 正五角形の性質 三角形の相似 黄金比 等脚台形 ひし形 受験の月




通常の五角形の面積を求める 3つの方法 Wikihow



不規則な五角形の面積の求め方を教えて下さい 不規則な五角形 平 Yahoo 知恵袋



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典




正五角形の長さや面積の導出 数学の偏差値を上げて合格を目指す




小学5年生 正多角形 算数 Active Learning 学院




つくばサイエンスエッジ18 文京学院大学女子高校 みらいぶ 高校生サイト




面積 面積の求め方のくふう 01 面積の公式を使って Youtube




面積の求め方が一向に分かりません 教えていただけると嬉しいです Clearnote



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス




正方形に内接する面積最大の正五角形 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog




半径2の円に内接する正五角形の一辺の長さ の求め方 Youtube
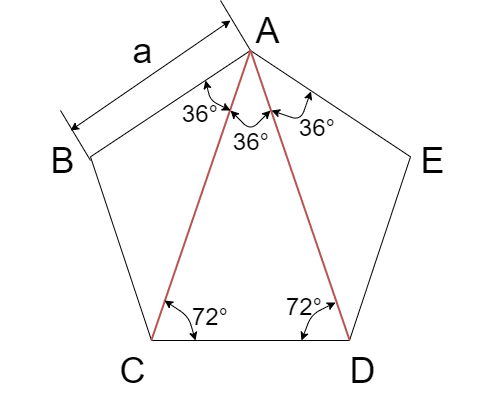



正多角形の面積公式一覧と導出方法を解説 正二十四角形まで
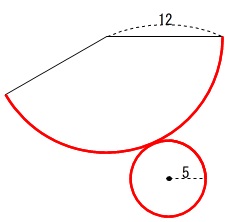



円錐 すい の表面積や四角錐 五角錐の体積の求め方



多角形の面積




最も好ましい 五角形 の 面積 の 求め 方 シモネタ
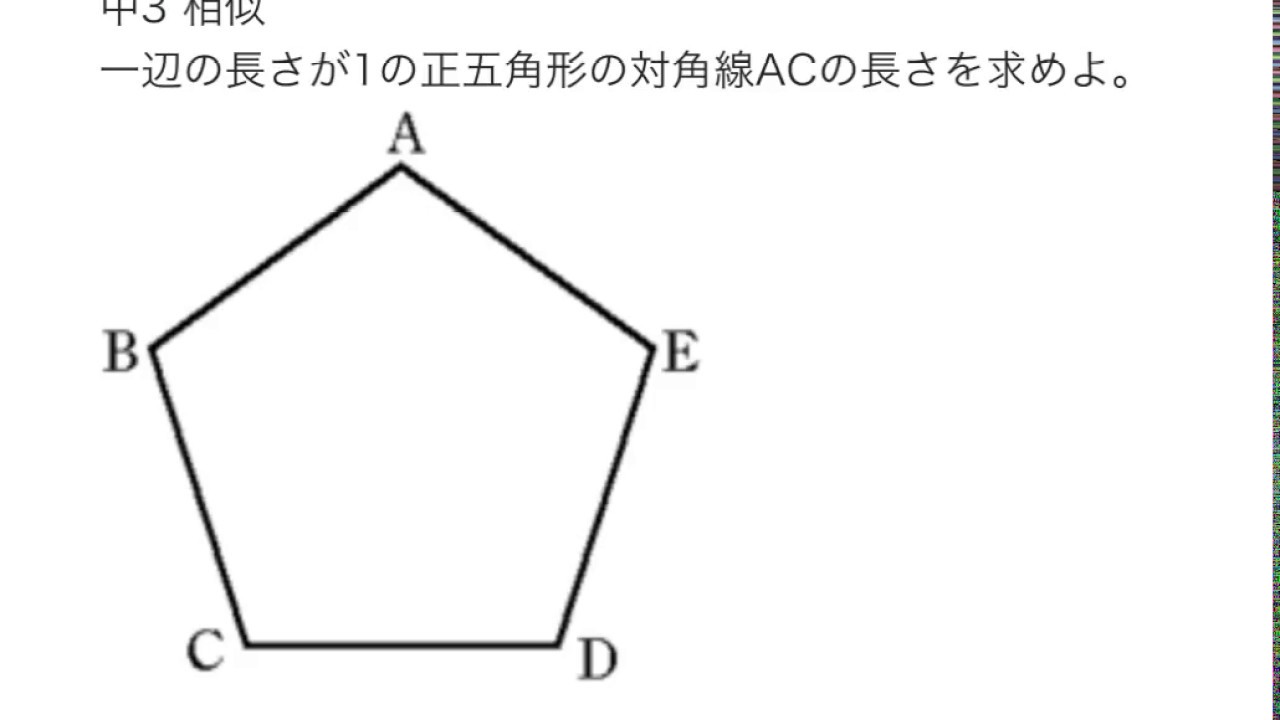



中3相似 正五角形の対角線の長さを求める問題 Youtube




通常の五角形の面積を求める 3つの方法 Wikihow
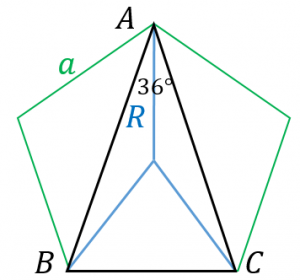



正五角形の面積を求める2つの公式 具体例で学ぶ数学




高校数学 正多角形の面積の求め方 例題編 映像授業のtry It トライイット




昔作った問題 3 五角形の面積の求め方を簡単な日本語で説明させる Baruku07のブログ



0 件のコメント:
コメントを投稿